一篇很久之前写的文章了，不过过了这么多年，模拟退火由于其效果和实现简单的优势，依然是智能算法中一个比较热门的算法，故老博客搬运而来。

简介

模拟退火算法从外部来看就是一个优化问题的解析器,我们给他传递初始解和产生新解的方法,它就能不断产生新解,并比较最终返回一个近似最优解.由于数学建模对算法的时间限制不严,而模拟退火又较易于实现,因此它也是数学建模里较常用的一种智能算法.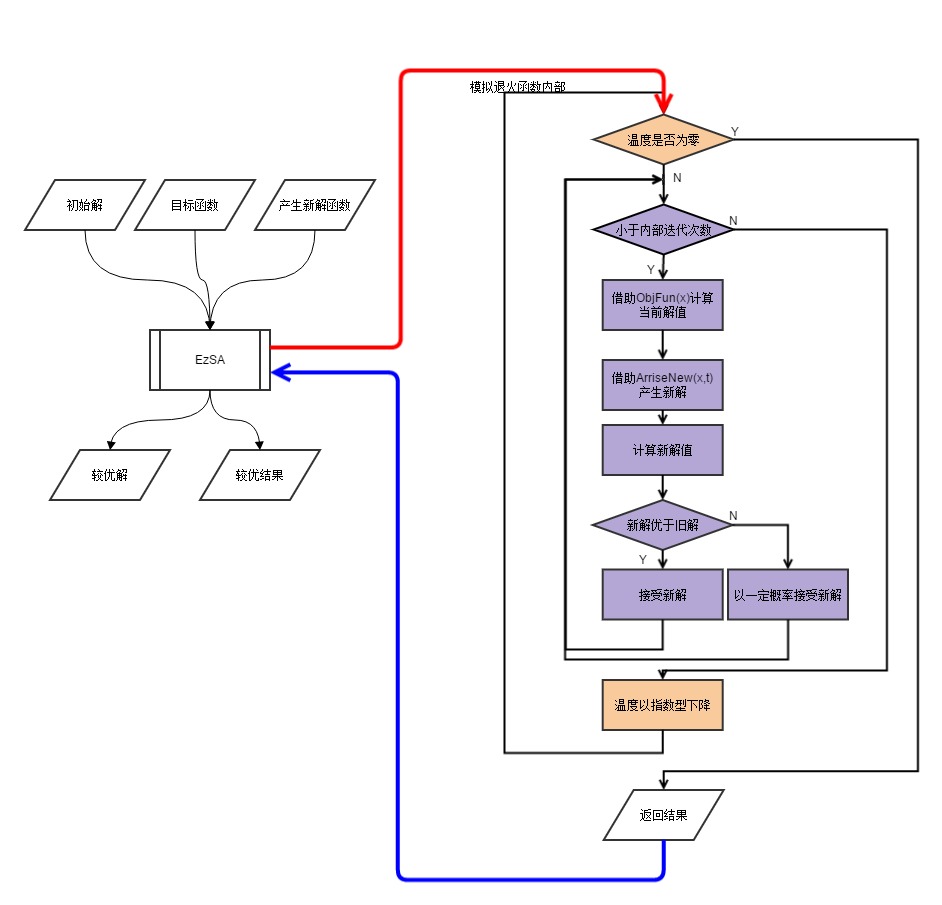

快速使用

在介绍具体算法前,我们完全可以在短时间内使用上模拟退火.

例1:求`min(x^2+y^2),x,y∈R`.

首先,我们提供一个初始解.文件main.m.
1
x=[2,2];
其次,构造出一个评价函数(或称目标函数).文件OptFun.m.
1
2
3
function y=OptFun(x)
y=x(1)^2+x(2)^2;
end
接着,构造一个能够不断根据旧解产生新解的函数.这里我们根据旧解以正态随机函数的形式产生新解.文件Arrise.m.
1
2
3
4
function X=Arrise(x)
X(1)=normrnd(x(1),2);
X(2)=normrnd(x(2),2);
end
复制EzSA.m到文件夹.
最后,调用现成的模拟退火函数EzSA.文件main.m.
1
[ x,res ]=EzSA(x,@myFirstSA,@Arrise)
如果你看到一个进度条,那么恭喜你,你已经会使用模拟退火算法了!

让我们看看结果:

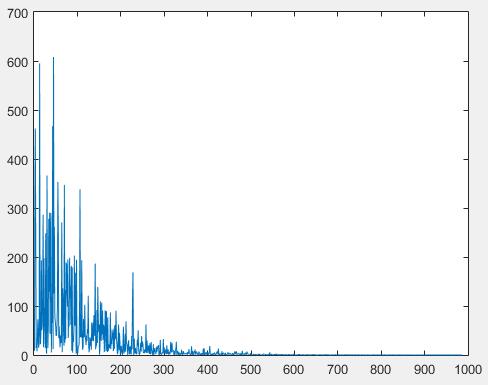
图像记载了我们之前尝试的解值,可以看出在数次迭代后数值处于稳定状态,表示这次模拟退火算法成功了.

同时,x 返回较优解,res返回较优值.
1
2
3
4
x =
-0.0035 -0.0027
res =
1.9562e-05

让我们总结一下模拟退火函数的使用步骤:

提供或初始化一个初始解.
构造出一个评价函数(或称目标函数),该函数接收解,并返回一个数值(视值越小解越优).
构造一个能够不断根据旧解产生新解的函数(注意,这个函数的设计优劣直接影响到模拟退火效果的好坏).
调用现成的模拟退火函数EzSA(初始解,评价函数句柄,产生新解函数句柄).
一段时间后模拟退火算法结束,返回较优解和解值

例2:旅行商问题(TSP)

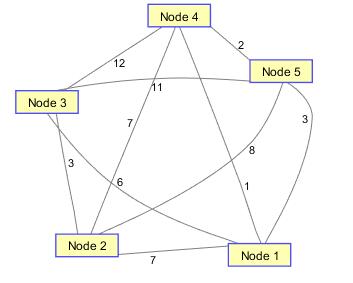
现有五个城市,彼此间距离如图所示,现在旅行商需要经过所有城市一次并回到出发点.我们需要为他规划最短路线.

graph

首先,以邻接矩阵存储图并提供初始解.文件main.m.

global n    %n为城市数,由于在无法将n以参数形式传递给计算距离的函数,故声明为全局变量
global graph %同上
n=5;
graph=[0,7,6,1,3;7,0,3,7,8;6,3,0,12,11;1,7,12,0,2;3,8,11,2,0];

city=1:5; %初始解

其次是评价函数,设city为五个城市的访问顺序.文件computerTour.m.

function len=computerTour(city)   %计算路线总长度，每个城市只计算和下家城市之间的距离。
    global n %获取n为城市数
    global graph
    len=0;
    for i=1:n-1
        len=len+graph(city(i),city(i+1));
    end
    len=len+graph(city(n),city(1));
end

接着,根据旧解产生新解的函数.文件perturbTour.m.

function city=perturbTour(city)
    %随机置换两个不同的城市的坐标
    %产生随机扰动
    global n
    p1=randi([1,n]);
    p2=randi([1,n]);
    tmp=city(p1);
    city(p1)=city(p2);
    city(p2)=tmp;
end

最后,调用模拟退火函数(与第一步写在同一文件),并运行.文件main.m
1
[city,res]=EzSA(city,@computerTour,@perturbTour)

结果:

city =
    4     1     3     2     5
res =
    20

原理讲解

源代码:

function [X resEnd]=EzSA(X,ObjFun,ArriseNew,iter,zero)
    [ra,co]=size(X);
    RES=[ObjFun(X)];  %每次迭代后的结果
    temperature=100*co;      %初始温度
    if nargin==3
        zero=1e-2;
        iter=5e2;               %内部蒙特卡洛循环迭代次数
    end
    if nargin==4
        zero=1e-2;
    end

    h=waitbar(0,'SAing....');
    while temperature>zero    %停止迭代温度
        for i=1:iter     %多次迭代扰动，一种蒙特卡洛方法，温度降低之前多次实验
            preRes=ObjFun(X);         %目标函数计算结果
            tmpX=ArriseNew(X);      %产生随机扰动
            newRes=ObjFun(tmpX);     %计算新结果

            delta_e=newRes-preRes;  %新老结果的差值，相当于能量
            if delta_e<0        %新结果好于旧结果，用新路线代替旧路线
                X=tmpX;
            else                        %温度越低，越不太可能接受新解；新老距离差值越大，越不太可能接受新解
                if exp(-delta_e/temperature)>rand() %以概率选择是否接受新解 p=exp(-ΔE/T)
                    X=tmpX;      %可能得到较差的解
                end
            end
        end
        RES=[RES ObjFun(X)];
        temperature=temperature*0.99;   %温度不断下降
        waitbar((log(temperature/(100*co))/log(0.99))/(log(zero/(100*co))/log(0.99)),h,sprintf('Now Temperature:%.2f',temperature));
    end
    close(h)
    plot(RES);
    resEnd=RES(end);
end

结合代码再看开头的流程图.

初始化,计算初始解的解值,设置初始温度.
模拟退火结构上就是两重循环,外部循环检查温度并降温,内部不断地产生新解并与旧解比较.

若新解优于旧解则新解无条件被旧解替代.
否则,有一定概率(exp(-ΔE/T))新解取代旧解.注意这个环节正是模拟退火能跳脱局部最优解,取得全局最优解的关键.

由此,我们可以得知影响模拟退火效果的主要因素有:

终止温度.一般上,终止温度越低,取得解越优.
内部迭代次数.一般上,内部迭代次数越多,取得解越优.
产生新解函数.

总结

模拟退火是对热力学退火过程的模拟,使算法在多项式时间内能给出一个近似最优解.由于MATLAB自带的模拟退火工具箱调用复杂且执行效果不理想,本文给出了较简单的函数原型和调用方法.该算法也包含以下优缺点(个人见解):

优点:

相较于一般的蒙特卡洛算法,有更少的尝试次数,同时实现上并不比蒙特卡洛花更多时间.
相较于遗传算法等大型智能算法,模拟退火实现简单,并能返回较满意的结果.
目标函数可以自己定制,相较于普通的规划解析器,模拟退火能适用于更广的范围(NPC问题,甚至给给神经网络做优化).
对于离散型的变量有更优秀的效果.

缺点:

内部本质上还是蒙特卡洛算法,新解与旧解本质上无关联.
相较于遗传算法,模拟退火难以控制算法的运行时间,EzSA的后面两个可选参数就是内部迭代次数和0度温度.而迭代次数给少了效果不理想,给多了有会增加等待时间.
对连续型的规划问题效果并不好.

样例和函数原型下载:
https://github.com/Anemone95/matlab-sa

简介

快速使用

例1:求min(x^2+y^2),x,y∈R.

例2:旅行商问题(TSP)

原理讲解

总结

例1:求`min(x^2+y^2),x,y∈R`.