遗传算法是求解近似最优解的最具代表性的智能算法之一,如今的很多方法都可以看到它的影子,比如说之前在研究的基于覆盖率的fuzz测试,其中的输入变异就类似于遗传算法,故从旧博客搬运来。
简介
遗传算法在外部体现同模拟退火一样,也是属于优化问题的一个求解器.但由于其优异的收敛速度和比模拟退火更优秀的结果,在对结果要求高的题目上,它也成为我们求解问题的常用方法.
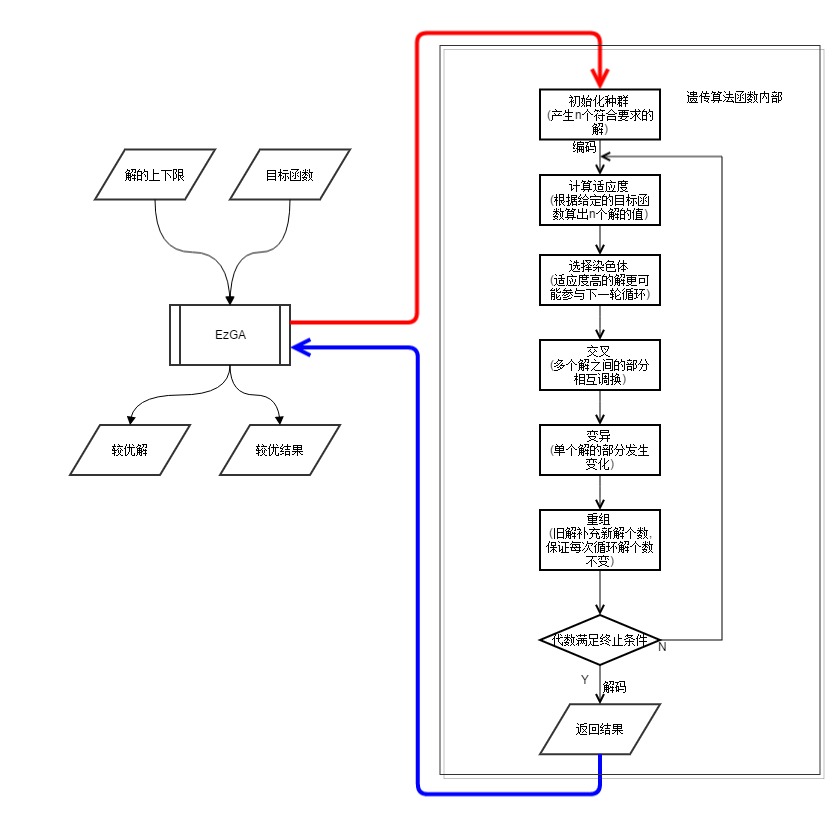
快速使用
遗传算法在实现上比模拟退火要复杂很多,但若不关心其内部算法,使用上反而比模拟退火要简单.
连续型随机变量
案例一:求min(x^2+y^2),x,y∈[-1e5,1e5]:
复制
GANorm文件夹到你的工作目录.同文件夹下新建
demo.m文件,输入:1
2y=@(x)x(1)^2+x(2)^2;
[best,x]=EzGA([-1e5 1e5;-1e5 1e5],y)运行
demo.m文件,得到从运行及结果:1
2
3
4
5
6sizepop =
1000
best =
3.9901
x =
1.9975 -0.0001没错,简单的遗传算法函数的调用形式为EzGA(变量上下限,目标函数句柄[,初始种群数量=500,附加数据]),注意第三个,第四个变量为可选参数.
案例二:求min(0.7*x(1)+0.8*x(2)),x,y∈[-1e5,1e5]:
复制
GANorm文件夹到你的工作目录.同文件夹下新建
demo2.m文件,输入:1
[best,x]=EzGA([-1e5 1e5;-1e5 1e5],@OptFun,1e2,[0.7 0.8])
同文件夹下新建
OptFun.m文件,输入:1
2
3function y=OptFun(x,coe)
y=coe(1)*x(1)^2+coe(2)*x(2)^2;
end运行
demo2.m文件,得到从运行及结果:1
2
3
4
5
6
7sizepop =
100
best =
1.1761e-07
x =
1.0e-03 *
-0.0079 0.3834
原理讲解
以下结合案例,来解释一下遗传算法的具体实现.
连续型随机变量(TSP问题)
下面又是我们的旅行商问题,同样,我们有图(*代表城镇):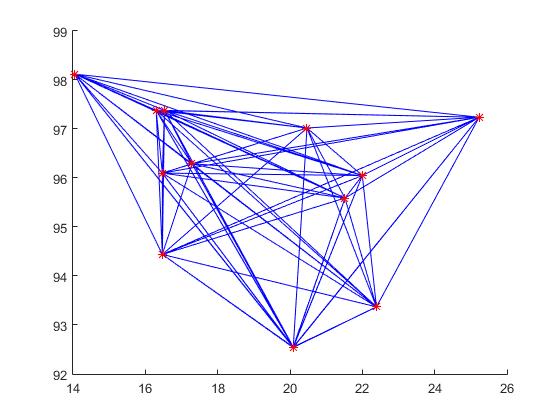
首先,结合流程图,我们首先写主函数调用遗传算法GATSP1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19%记录了城镇的坐标
X=[
16.47,96.10
16.47,94.44
20.09,92.54
22.39,93.37
25.23,97.24
22.00,96.05
20.47,97.02
17.29,96.29
16.30,97.38
14.05,98.12
16.53,97.38
21.52,95.59
20.09,92.55];
D=Distance(X); %取得邻接矩阵
N=size(D,1); %城镇数
%调用遗传算法
[obj,x]=GATSP(N,D);
遗传算法主函数:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46function [minObj,x]=GATSP(N,attach,NIND)
MAXGEN=200;
if nargin<3
NIND=100;
end
Pc=0.9;
Pm=0.2;
GGAP=0.9;
Chrom=InitPop(NIND,N);
% Rlength=PathLength(D,Chrom(1,:));
gen=0;
% ObjV=PathLength(D,Chrom);
% preObjV=min(ObjV);
history=[];
h=waitbar(0,'Evolving....');
while gen<MAXGEN
ObjV=PathLength(attach,Chrom);
% min(ObjV)
FitnV=Fitness(ObjV);
SelCh=Select(Chrom,FitnV,GGAP);
SelCh=Recombin(SelCh,Pc);
SelCh=Mutate(SelCh,Pm);
SelCh=Reverse(SelCh,attach);
Chrom=Reins(Chrom,SelCh,ObjV);
history=[history min(ObjV)];
gen=gen+1;
waitbar(gen/MAXGEN,h,sprintf('Now Generation:%d',gen));
if gen>30
if sum(diff(history(end-30:end)))==0
break
end
end
end
close(h)
ObjV=PathLength(attach,Chrom);
plot(history)
title('Fitness curve','fontsize',12);
xlabel('Evolutionary generation','fontsize',12);ylabel('Option','fontsize',12);
% axis([0,MAXGEN,0,1])
[minObj,minInd]=min(ObjV);
x=Chrom(minInd,:);
end
初始化种群
初始化种群实际就是产生NIND个符合要求的解.InitPop.m:1
2
3
4
5
6
7
8function Chrom=InitPop(NIND,N)
%NIND 种群大小
%N 单个染色体长度(城市个数)
Chrom=zeros(NIND,N);
for i=1:NIND
Chrom(i,:)=randperm(N); %随机产生种群
end
end
适应度函数
TSP的要求是路程最短,而适应度函数视值越大越优,所以我们这里先计算出长度后,再对其取反.
PathLength.m:1
2
3
4
5
6
7
8
9
10
11
12function len=PathLength(graph,Chrom)
[row,col]=size(graph);
NIND=size(Chrom,1);
len=zeros(NIND,1);
for i=1:NIND
% path
p=[Chrom(i,:) Chrom(i,1)];
i1=p(1:end-1);
i2=p(2:end);
len(i,1)=sum(graph((i1-1)*col+i2));% ∑graph(from,to)
end
end
Fitness.m:1
2
3
4function FitnV=Fitness(len)
% len 个体长度
FitnV=1./len;
end
选择操作
模拟自然选择,实际上就是指适应度越好的解被留下来的几率越大(但也不是说适应度不好的解不被留下).1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20function SelCh=Select(Chrom,FitnV,GGAP)
%种群 适应值 选择概率 被选择个体
NIND=size(Chrom,1);
NSel=max(floor(NIND*GGAP+0.5),2);
Chrlx=Sus(FitnV,NSel);
SelCh=Chrom(Chrlx,:);
end
function NewChrlx=Sus(FitnV,NSel)
%适应值 数目
%备选索引
[Nind,ans_]=size(FitnV);
cumfit=cumsum(FitnV);
trials=cumfit(Nind)/NSel*(rand+(0:NSel-1)');
Mf=cumfit(:,ones(1,NSel));
Mt=trials(:,ones(1,Nind))';
[NewChrlx,ans_]=find(Mt<Mf&[zeros(1,NSel);Mf(1:Nind-1,:)]<=Mt);
[ans_,shuf]=sort(rand(NSel,1));
NewChrlx=NewChrlx(shuf);
end
交叉操作
模拟染色体的交叉现象,注意在这里会出现城市出现重复的现象,需要用部分映射的方法消除冲突(介于篇幅不赘述,但我就记得这问题我想了一下午,然后一个数科院的妹子3分钟搞定了.顿时就感觉!!).
原先的两个解:1
2
3| 9, 5, 1| 3, 7, 4, 2| 10, 8, 6|
|--------|-----------|---------|
|10, 5, 4| 6, 3, 8, 7| 2, 1, 9|
交叉1
2
3| 9, 5, 1| 6, 3, 8, 7| 10, *, *|
|--------|-----------|---------|
|10, 5, *| 3, 7, 4, 2| *, 1, 9|
部分映射1
2
3| 9, 5, 1| 6, 3, 8, 7| 10, 4, 2|
|--------|-----------|---------|
|10, 5, 8| 3, 7, 4, 2| 6, 1, 9|
Recombin.m:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36function SelCh=Recombin(SelCh,Pc)
%被选择个体 概率
%交叉后个体
NSel=size(SelCh,1);
for i=1:2:NSel-mod(NSel,2)
if Pc>=rand
[SelCh(i,:),SelCh(i+1,:)]=intercross(SelCh(i,:),SelCh(i+1,:));
end
end
end
function [a,b]=intercross(a,b)
L=length(a);
r1=randsrc(1,1,[1,L]);
r2=randsrc(1,1,[1,L]);
if r1~=r2
a0=a;b0=b;
s=min([r1,r2]);
e=max([r1,r2]);
for i=s:e
a1=a;b1=b;
a(i)=b0(i);
b(i)=a0(i);
x=find(a==a(i));
y=find(b==b(i));
i1=x(x~=i);
i2=y(y~=i);
if ~isempty(i1)
a(i1)=a1(i);
end
if ~isempty(i2)
b(i2)=b1(i);
end
end
end
end
变异操作
模拟染色体的变异现象,这里的算子就是两个随机位置上的数交换1
2| 9, 5, 1| 3, 7, 4, 2| 10, 8, 6|
| 9, 5, 2| 3, 7, 4, 1| 10, 8, 6|
Mutate.m:1
2
3
4
5
6
7
8
9
10function SelCh=Mutate(SelCh,Pm)
%个体 概率
[NSel,L]=size(SelCh);
for i=1:NSel
if Pm>=rand
R=randperm(L);
SelCh(i,R(1:2))=SelCh(i,R(2:-1:1));
end
end
end
重组
就是把经过选择,交叉,变异的解与旧解混合,保证种群内个体数不变.1
2
3
4
5
6function Chrom=Reins(Chrom,SelCh,ObjV)
NIND=size(Chrom,1);
NSel=size(SelCh,1);
[TobjV,index]=sort(ObjV);
Chrom=[Chrom(index(1:NIND-NSel),:);SelCh];
end
反转(不必要掌握)
反转操作是针对TSP问题对于局部的一种优化,本身不在遗传算法范围内.这里给出算法代码.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15function SelCh=Reverse(SelCh,D)
[row,col]=size(SelCh);
ObjV=PathLength(D,SelCh);
SelCh1=SelCh;
for i=1:row
r1=randsrc(1,1,[1:col]);
r2=randsrc(1,1,[1:col]);
mininverse=min([r1 r2]);
maxinverse=max([r1 r2]);
SelCh1(i,mininverse:maxinverse)=SelCh1(i,maxinverse:-1:mininverse);
end
ObjV1=PathLength(D,SelCh1);
index=ObjV1<ObjV;
SelCh(index,:)=SelCh1(index,:);
end
小结
遗传算法是一个模拟生物遗传进化的,比较成熟的大型智能算法.采用设计好的算子,可以解决大部分类型的规划问题.但由于其算法较为复杂,在比赛中没有充分把握还是要谨慎使用.
本文借助三个案例,大致介绍了遗传算法的工作原理,同时对两大典型的规划问题给出了简单可调用的函数原型.方便大家学习使用.
同时,遗传算法的优劣总结如下(个人观点):
优点
- 相对于新型的智能算法,如:粒子群算法,蚁群算法.他更加成熟稳定.这表现在可适用的问题类型众多(蚁群不能算TSP).
- 相对于模拟退火算法,它不用给出初始值和重组解的方式,而是交给算法本身完成.使用时只需给定目标函数和解的限制条件.
- 相对于模拟退火,它有更优秀的收敛时间,可控的时间复杂度.并在连续型随机变量上有明显优势.
- 相对于传统算法,有一定的定制空间,自己定制的目标函数能适用于matlab的各种函数(包括给神经网络做优化).
缺点
- 相对于新型智能算法,它收敛速度和结果差强人意.
- 相对于能够定制解的模拟退火,遗传算法不够灵活.
- 整体算法实现复杂,且由于算子众多,学习成本大.若在比赛中不能将问题转化成文中介绍的两种类型,不建议使用该算法.
参考书籍:《MATLAB智能算法30个案例分析》
程序下载: https://github.com/Anemone95/matlab-GA